Bei einer hypothesenprüfenden Zielsetzung geht man von einer bestimmten Metrik und einer bestimmten Dimensionalität aus und kann dann anhand von Daten den Bestätigungsgrad dieser Hypothese prüfen. Beim hypothesensuchenden Vorgehen fragt man dagegen, durch welche Konfiguration bestimmter Metrik und Dimensionalität die Ausgangsdaten am besten approximiert werden. Indem man die Skalierungsprozedur mit verschiedener Metrik und unterschiedlicher Dimensionalität wiederholt, kann man ein geeignetes Modell identifizieren (nämlich dasjenige mit dem niedrigsten Stress).Problematisch hierbei ist allerdings, daß bei der Bestimmung des Stress möglicherweise das globale Minimum nicht gefunden wird, wenn die Schätzprozedur an einem lokalen Minimum hängenbleibt.
Es existieren aber auch Maße der Anpassungsgüte, die ohne das Konzept der Disparitäten ![]() auskommen: Die metrische Determination M (metric determinance nach Shepard) bezeichnet die Korrespondenz zwischen der ``wahren'' Konfiguration
auskommen: Die metrische Determination M (metric determinance nach Shepard) bezeichnet die Korrespondenz zwischen der ``wahren'' Konfiguration ![]() und der errechneten Konfiguration X bzw. zwischen ``wahren'' und rekonstruierten Distanzen. Die wahren Konfigurationen sind allerdings nur in Ausnahmefällen bekannt, beispielsweise bei Monte-Carlo-Untersuchungen zur Angemessenheit nonmetrischer MDS-Prozeduren. Die metrische Determination M kann als Determinationskoeffizient bestimmt werden, d.h. als quadrierte Produkt-Moment-Korrelation zwischen den euklidischen Distanzen aus der wahren und aus der abgeleiteten Konfiguration.
und der errechneten Konfiguration X bzw. zwischen ``wahren'' und rekonstruierten Distanzen. Die wahren Konfigurationen sind allerdings nur in Ausnahmefällen bekannt, beispielsweise bei Monte-Carlo-Untersuchungen zur Angemessenheit nonmetrischer MDS-Prozeduren. Die metrische Determination M kann als Determinationskoeffizient bestimmt werden, d.h. als quadrierte Produkt-Moment-Korrelation zwischen den euklidischen Distanzen aus der wahren und aus der abgeleiteten Konfiguration.
Um die MDS formal einführen zu können, sind zunächst einige Definitionen erforderlich:
![]()
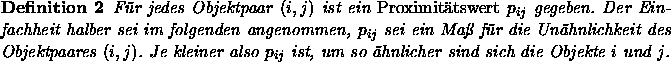

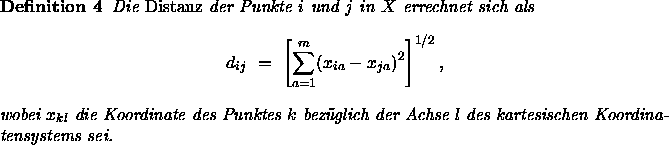
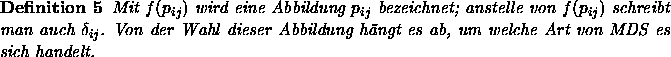
Nun sollen verschiedene Möglichkeiten für die Wahl der Funktion f und die dazugehörigen MDS-Modelle aufgezählt werden:
![]()
bzw. im verallgemeinerten Fall mit Missing Data
![]()
![]()
Bezeichnet ![]() die m Koordinaten des Punktes i und entsprechend
die m Koordinaten des Punktes i und entsprechend ![]() die m Koordinaten des Punktes j, die zu finden sind, und g die Distanzformel, dann läßt sich auch etwas ausführlicher schreiben
die m Koordinaten des Punktes j, die zu finden sind, und g die Distanzformel, dann läßt sich auch etwas ausführlicher schreiben
![]()
![]()
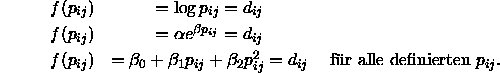
Die gerade beschriebenen Modelle sind aber nur von eingeschränktem praktischen Nutzen, da sie keine Meßfehler bei der Bestimmung der Proximitäten berücksichtigen. Borg (1981) geht in diesem Zusammenhang von der vereinfachenden Annahme aus, die Antworten der Versuchspersonen würden zufällig um einen wahren Wert streuen. Neben der Berücksichtigung des Meßfehlers sollte die MDS aber auch externe Relevanzgesichtspunkte berücksichtigen: Da kaum eine exakte Passung der gefundenen Konfiguration an das gewählte Modell zu erzielen ist, muß man sich damit zufrieden geben, daß eine gefundene Konfiguration das gewählte MDS-Modell ``fast'' erfüllt. Letztlich läuft dies darauf hinaus, die MDS-Modell von ![]() zu
zu ![]() zu lockern, wobei
zu lockern, wobei ![]() als ``ausreichend genau'' zu lesen ist. Die bisher beschriebenen iterativen Verfahren zur Bestimmung der MDS-Lösung führen ebenfalls meist nicht zu einer perfekten Lösung, sondern nur zu einer approximativ perfekten.
als ``ausreichend genau'' zu lesen ist. Die bisher beschriebenen iterativen Verfahren zur Bestimmung der MDS-Lösung führen ebenfalls meist nicht zu einer perfekten Lösung, sondern nur zu einer approximativ perfekten.
Um den im letzten Absatz beschriebenen Ungenauigkeiten Rechnung zu tragen, definiert man ein Fehlermaß ![]() als
als
![]()
bzw. (wegen der Definition ![]() )
)
![]()
Der Gesamtfehler ![]() einer MDS-Lösung ergibt sich dann Summe aller einzelnen Fehler
einer MDS-Lösung ergibt sich dann Summe aller einzelnen Fehler ![]() :
:
![]()
oder einfacher
![]()
Dieses allgemeine Fehlermaß ist allerdings maßstabsabhängig. Deshalb erfolgt eine Normierung, indem der Fehlerwert durch die Summe der quadrierten Distanzen ![]() geteilt wird.
geteilt wird.![]() Zieht man noch die Wurzel aus dem so erhaltenen Koeffizienten, erhält man den sogenannten Stress S als Fehlermaß:
Zieht man noch die Wurzel aus dem so erhaltenen Koeffizienten, erhält man den sogenannten Stress S als Fehlermaß:

Der Stress ist bei einer perfekten Lösung, für die gelten muß ![]() , gleich Null. Vom mathematischen Standpunkt aus gibt es nur einen Grund dafür, daß der Stress von Null verschieden ist, nämlich ungenügende Dimensionalität. Vom inhaltlichen Standpunkt sind dagegen zwei Ursachen für Stress denkbar: unzureichende Dimensionalität oder zufällige (unsystematische) Meßfehler. Kennt man die ``wahre'' Dimensionalität, dann erlaubt der Stress eine Abschätzung dieses Meßfehlers.
, gleich Null. Vom mathematischen Standpunkt aus gibt es nur einen Grund dafür, daß der Stress von Null verschieden ist, nämlich ungenügende Dimensionalität. Vom inhaltlichen Standpunkt sind dagegen zwei Ursachen für Stress denkbar: unzureichende Dimensionalität oder zufällige (unsystematische) Meßfehler. Kennt man die ``wahre'' Dimensionalität, dann erlaubt der Stress eine Abschätzung dieses Meßfehlers.
Der Stress stellt ein normiertes Maß für die Restvarianz einer monotonen Regression von Distanzen auf Unähnlichkeiten bei gewählter Ausgangskonfiguration dar; er ist analog zu dem Standardschätzfehler bei der bivariaten Regression. Bei der linearen Regressionsanalyse will man eine Gerade finden, die einen Punkteschwarm möglichst gut beschreibt, bei der nichtmetrischen MDS nach Kruskal werden dagegen die Punkte der Konfiguration so lange verschoben, bis sie auf einer Geraden zu liegen kommen (cf. Dunn-Rankin, 1983).
Der raw stress ![]() ist invariant gegenüber Rotation, Translation und Reflexion der Konfiguration, nicht jedoch gegenüber Strecken und Stauchen der Skalen. Da bei ordinalen Verfahren das Maß der Anpassungsgüte aber invariant gegenüber einer Vergrößerung der Konfiguration sein sollte, normiert man den ``rohen Stress'' an der Summe der tatsächlichen Distanzen
ist invariant gegenüber Rotation, Translation und Reflexion der Konfiguration, nicht jedoch gegenüber Strecken und Stauchen der Skalen. Da bei ordinalen Verfahren das Maß der Anpassungsgüte aber invariant gegenüber einer Vergrößerung der Konfiguration sein sollte, normiert man den ``rohen Stress'' an der Summe der tatsächlichen Distanzen ![]() und erhält so den (normierten) Stress.
und erhält so den (normierten) Stress.
Der Stress stellt ein deskriptives Maß für die Anpassungsgüte der Skalierung dar. Ahrens (1974) bezeichnet einen Stress von 0.1 als ausreichend, einen Stress von 0.05 als gut und einen Stress von 0.025 als exzellent. Ein wichtiger Aspekt bei der Bestimmung des Stress ist, daß dazu bereits die Anzahl n der Dimensionen und die Metrik der Distanzfunktion bekannt sein müssen. Dies hat nicht nur formale Konsequenzen, sondern auch theoretisch-inhaltliche Konsequenzen für das Skalierungsergebnis. Die Dimensionalität sollte so gewählt werden, daß die Einführung zusätzlicher Dimensionen keine deutliche Reduktion des Stress mehr bewirkt.
Neben dem Stress ist noch ein anderer Fehlerkoeffizient weit verbreitet. Er wird als Alienationskoeffizient K bezeichnet und ist nur bei Verwendung von Rank Images als Zieldistanzen geeignet. Man erhält ihn, indem man in der Formel für den Stress ![]() setzt (wobei
setzt (wobei ![]() eine einzelne Zelle des Rank Image bezeichnet) und anstelle von
eine einzelne Zelle des Rank Image bezeichnet) und anstelle von ![]() den Ausdruck
den Ausdruck ![]() schreibt. Somit gilt:
schreibt. Somit gilt:
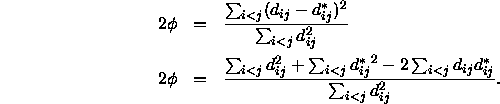
Setzt man in dieser Gleichung ![]() , dann folgt hieraus
, dann folgt hieraus
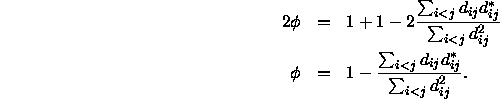
Der Term ![]() wird als Monotonizitätskoeffizient
wird als Monotonizitätskoeffizient ![]() bezeichnet. Er ist eine Art Korrelationsmaß, was sich besonders deutlich zeigt, wenn man ihn ähnlich der Definition der Korrelation formuliert:
bezeichnet. Er ist eine Art Korrelationsmaß, was sich besonders deutlich zeigt, wenn man ihn ähnlich der Definition der Korrelation formuliert:
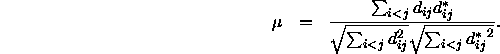
Der Monotonizitätskoeffizient ![]() unterscheidet sich also von einem (Produkt-Moment-)Korrelationskoeffizient nach Pearson nur dadurch, daß die Mittelwerte der Variablen ``Distanzen''
unterscheidet sich also von einem (Produkt-Moment-)Korrelationskoeffizient nach Pearson nur dadurch, daß die Mittelwerte der Variablen ``Distanzen'' ![]() und ``Rank Images''
und ``Rank Images'' ![]() nicht subtrahiert werden. Die Regressionsgeraden laufen somit durch den Ursprung und nicht durch den Schwerpunkt des Image-Diagramms.
nicht subtrahiert werden. Die Regressionsgeraden laufen somit durch den Ursprung und nicht durch den Schwerpunkt des Image-Diagramms.
In Übereinstimmung mit der statistischen Terminologie kann man ![]() als Determinationskoeffizienten bezeichnen, also als ein Maß für die erklärte Varianz im Image-Diagramm. Der Alienationskoeffizient K ist dann die Standardabweichung der unerklärten Streuung:
als Determinationskoeffizienten bezeichnen, also als ein Maß für die erklärte Varianz im Image-Diagramm. Der Alienationskoeffizient K ist dann die Standardabweichung der unerklärten Streuung:
![]()
Ähnlich wie für den Streß S gilt auch für den Alienationskoeffizienten K, daß eine perfekte Lösung zu K = 0 führt. Je größer K bzw. S werden, desto schlechter erfüllt eine Konfiguration das jeweilige MDS-Modell.
Eine weitere wichtige Bedeutung der Koeffizienten S und K liegt darin, daß aus ihnen ein iteratives Korrekturverfahren abgeleitet werden kann, das gänzlich unabhängig von den im ersten Kapitel beschriebenen geometrischen ad-hoc Überlegungen ist. Dieses sogenannte Gradientenverfahren wird im nächsten Abschnitt dargestellt.
Ahrens (1974) stellt die axiomatische Begründung der MDS durch Beals, Krantz und Tversky dar. Eine Menge von Axiomen enthält die Bedingungen, unter denen eine metrische Repräsentation von Unähnlichkeiten möglich ist, es werden also spezielle metrische Eigenschaften der isomorphen Abbildung eines empirischen Relativs in ein numerisches Relativ untersucht. Scheinbar ist nur eine bestimmte Klasse von Metriken sinnvoll verwendbar, nämlich Metriken mit additiven Segmenten, bei denen Distanzen entlang einer kürzesten Kurve (Segment) additiv sind. Die Minkowski-Metriken erfüllen diese Anforderung.
Ein weiterer Satz von Axiomen betrifft die dimensionale Repräsentation von Unähnlichkeiten. Diese impliziert die prinzipielle Forderung nach der dimensionalen Zerlegbarkeit globaler Reizähnlichkeiten (decomposability). Außerdem soll das Modell die Reizdifferenzen innerhalb jeder Dimension abbilden (intradimensional subtractivity) und die interdimensionale Addition dieser spezifischen Reizunterschiede ermöglichen (interdimensional additivity). Das gesamte Dimensionsmodell vereinigt alle drei Gesichtspunkte und wird als additives Differenz-Modell bezeichnet.
Die Axiome zur Dimensionalität und zur Metrik lassen sich kombinieren zu einem allgemeinen geometrischen Modell mit additiven Segmenten, welches nur von den Minkowski-Metriken, die von der Form
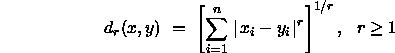
sind, erfüllt wird.
In diesem Abschnitt soll erklärt werden, wie aus einem Fehlermaß wie dem Stress S oder dem Alienationskoeffizient K ein Verfahren für MDS-Lösungen bestimmt werden kann, d.h. eine Konfiguration X und eine Transformation f gefunden werden können, die den Zusammenhang ![]() optimieren. Der Stress S wird dann minimiert, wenn der Fehlerterm
optimieren. Der Stress S wird dann minimiert, wenn der Fehlerterm ![]() minimal wird, wie an der Formel für den Stress erkennbar ist:
minimal wird, wie an der Formel für den Stress erkennbar ist:
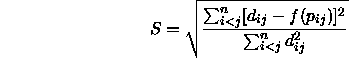
Um den Term ![]() zu minimieren, muß einerseits die Konfiguration X minimiert werden, andererseits muß auch die Funktion f minimiert werden. Deshalb geht man in einem Ping Pong Prozeß so vor, daß solange abwechselnd die beiden Terme minimiert werden, bis ein vorher gesetztes Abbruchkriterium erfüllt ist. Man verfolgt also folgende Strategie:
zu minimieren, muß einerseits die Konfiguration X minimiert werden, andererseits muß auch die Funktion f minimiert werden. Deshalb geht man in einem Ping Pong Prozeß so vor, daß solange abwechselnd die beiden Terme minimiert werden, bis ein vorher gesetztes Abbruchkriterium erfüllt ist. Man verfolgt also folgende Strategie:
Die verschiedenen MDS-Modelle sind durch die Art der Funktion f charakterisiert, weswegen die Bestimmung der Zieldistanzen ![]() ebenfalls vom jeweiligen MDS-Modell abhängt. Meist fällt die Bestimmung dieser Werte leicht: Bei der ordinalen MDS werden beispielsweise die Disparitäten berechnet und bei der Intervall-MDS können die einzelnen Werte von
ebenfalls vom jeweiligen MDS-Modell abhängt. Meist fällt die Bestimmung dieser Werte leicht: Bei der ordinalen MDS werden beispielsweise die Disparitäten berechnet und bei der Intervall-MDS können die einzelnen Werte von ![]() dadurch abgeleitet werden, daß die Parameter
dadurch abgeleitet werden, daß die Parameter ![]() und
und ![]() im Regressionsproblem
im Regressionsproblem ![]() für alle definierten
für alle definierten ![]() bestimmt werden.
bestimmt werden.
Nun setzt man in die Formel für den Stress die Definition der Distanzen durch die euklidische Distanz der Punkte ein, so daß man folgende Formel erhält,
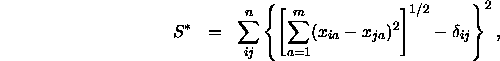
die minimiert werden soll. Dazu müssen also insgesamt ![]() Koordinaten
Koordinaten ![]() so bestimmt werden, daß
so bestimmt werden, daß ![]() möglichst klein wird. Dazu bedient man sich folgenden Tricks: Man betrachtet X nicht als Konfiguration von n Punkten im m-dimensionalen Raum, sondern als einen einzigen Punkt im
möglichst klein wird. Dazu bedient man sich folgenden Tricks: Man betrachtet X nicht als Konfiguration von n Punkten im m-dimensionalen Raum, sondern als einen einzigen Punkt im ![]() -dimensionalen Raum mit den Koordinaten
-dimensionalen Raum mit den Koordinaten ![]() oder kurz
oder kurz ![]() . Hierfür wird ebenfalls die Schreibweise X verwendet.
. Hierfür wird ebenfalls die Schreibweise X verwendet.
Nun stellt sich also die Aufgabe, X bezüglich seiner ![]() Koordinatenachsen so zu bewegen, daß
Koordinatenachsen so zu bewegen, daß ![]() minimiert wird. Da die Koordinatenachsen alle senkrecht aufeinander stehen, bleiben durch eine Bewegung von X bezüglich einer Achse k alle Koordinaten von X mit Ausnahme von
minimiert wird. Da die Koordinatenachsen alle senkrecht aufeinander stehen, bleiben durch eine Bewegung von X bezüglich einer Achse k alle Koordinaten von X mit Ausnahme von ![]() unverändert. Daher kann die gesuchte
unverändert. Daher kann die gesuchte ![]() -Minimierung in ein Vektorbündel aufgelöst werden, das aus
-Minimierung in ein Vektorbündel aufgelöst werden, das aus ![]() Bewegungen entlang der
Bewegungen entlang der ![]() Achsen besteht.
Achsen besteht.
Nun stellt man sich eine Funktion vor, deren Abszisse die Menge der möglichen ![]() aus der Konfiguration
aus der Konfiguration ![]() ist und deren Ordinate das Fehlermaß
ist und deren Ordinate das Fehlermaß ![]() darstellt. X ist dann so zu bewegen, daß alle seine Komponenten jeweils globale Minima werden. Die Extremwerte für jede Komponente
darstellt. X ist dann so zu bewegen, daß alle seine Komponenten jeweils globale Minima werden. Die Extremwerte für jede Komponente ![]() ergeben sich durch Ableiten und Nullsetzen der Fehlerfunktion
ergeben sich durch Ableiten und Nullsetzen der Fehlerfunktion ![]() . Die Ableitung von
. Die Ableitung von ![]() bezüglich einer einzelnen Variable
bezüglich einer einzelnen Variable ![]() ist dadurch möglich, daß alle
ist dadurch möglich, daß alle ![]() mit Ausnahme von
mit Ausnahme von ![]() als Konstanten betrachtet werden und daher die partielle Ableitung
als Konstanten betrachtet werden und daher die partielle Ableitung ![]() bestimmt wird. Setzt man diese Ableitung gleich Null, gelangt man zu folgender Gleichung (cf. Borg, 1981):
bestimmt wird. Setzt man diese Ableitung gleich Null, gelangt man zu folgender Gleichung (cf. Borg, 1981):
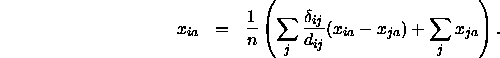
Man kann X grundsätzlich ``zentrieren'', also die Mittelwerte der Punkte auf allen m Koordinatenachsen in den Ursprung des Koordinatensystems legen. Damit wird ![]() und die letzte Gleichung vereinfacht sich zu
und die letzte Gleichung vereinfacht sich zu
Für den Fall von i = j definiert man ![]() ; dasselbe gilt für den praktisch kaum anzutreffenden Fall, daß
; dasselbe gilt für den praktisch kaum anzutreffenden Fall, daß ![]() ist. Die Auflösung der Gleichung 3.1 nach
ist. Die Auflösung der Gleichung 3.1 nach ![]() ist nur zum Teil möglich, da ja
ist nur zum Teil möglich, da ja ![]() ersetzt werden muß durch
ersetzt werden muß durch
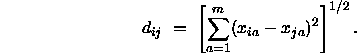
Die Extremwerte können somit nach der Gleichung 3.1 nur für gegebene Distanzen ![]() bestimmt werden, was das Problem der Minimierung von
bestimmt werden, was das Problem der Minimierung von ![]() nur unvollständig löst. Es ist aber ein schrittweises Verfahren denkbar, bei dem man die Gleichung für
nur unvollständig löst. Es ist aber ein schrittweises Verfahren denkbar, bei dem man die Gleichung für ![]() bei gegebenen Distanzen löst, dann die neuen Werte für
bei gegebenen Distanzen löst, dann die neuen Werte für ![]() berechnet, wieder für
berechnet, wieder für ![]() löst usw. Zur Vereinfachung der Lösung definiert man Hilfswerte
löst usw. Zur Vereinfachung der Lösung definiert man Hilfswerte ![]() (Korrekturfaktoren, correction) auf folgende Weise:
(Korrekturfaktoren, correction) auf folgende Weise:
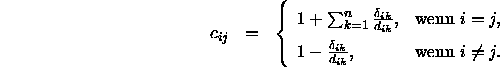
Damit vereinfacht sich die Gleichung 3.1 zu
![]()
oder, nach Einführung eines Iterationsindexes t, zu der Korrekturformel
![]()
In der ausführlichen Schreibweise lautet diese Formel
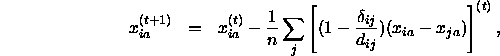
die genau der intuitiv-geometrisch gefundenen Gleichung 2.1 entspricht, bzw.
Man kann erkennen, daß die Koordinaten im Iterationsschritt (t+1) durch die entsprechenden Koordinaten und die entsprechende Ableitung zum Zeitpunkt (t) bestimmt sind. Wie man an Gleichung 3.2 erkennen kann, bewegt man sich bei einem Iterationsschritt vom Ausgangspunkt weg in Abhängigkeit von der partiellen Ableitung ![]() , also letztlich abhängig von der Steigung im Punkt
, also letztlich abhängig von der Steigung im Punkt ![]() . Hat man ein Minimum erreicht, ist diese Steigung aber gleich Null und das Minimum wird daher nicht mehr verlassen. Daraus ergibt sich auch der Nachteil dieses Verfahrens: Man kann an lokalen Minima hängenbleiben. Deshalb muß für das Iterationsverfahren eine geeignete Schrittgröße gewählt werden.
. Hat man ein Minimum erreicht, ist diese Steigung aber gleich Null und das Minimum wird daher nicht mehr verlassen. Daraus ergibt sich auch der Nachteil dieses Verfahrens: Man kann an lokalen Minima hängenbleiben. Deshalb muß für das Iterationsverfahren eine geeignete Schrittgröße gewählt werden.
Young (1987) schildert die Entwicklung und die Bedeutung der verschiedenen MDS-Methoden. Das erste vollständige MDS-Modell stammt von Torgerson (1952) und bestimmt aus einer Matrix fehlerfreier Distanzen die Dimensionalität der Distanzen und einen euklidischen Raum, in dem Punkte entsprechende Distanzen besitzen (nach dem Young-Householder-Theorem). Torgerson geht dabei von einer Matrix an Distanzen zwischen je zwei Objekten aus, die durch Finden eines geeigneten Nullpunkts in Verhältnisse von Entfernungen umgerechnet werden. Dann wird die Dimensionalität des psychologischen Raumes bestimmt sowie die Projektionen der Reize auf die Achsen dieses Raumes. Diesem metrischen Modell liegt ein euklidisches Modell zugrunde; es wurden aber bereits in den fünfziger Jahren Modelle mit einer City-Block-Metrik und mit einer allgemeinen Minkowski-Metrik entwickelt.
Shepard (1962) entwickelte die nichtmetrische MDS, die aus ordinalen Daten metrische Distanzen ermittelt und daher zu großem Interesse an der MDS führte. Grundlage ist eine feste monotone Funktion der Distanz. Shepard stellt die Methoden zur Verfügung, um die minimale Dimensionalität zu bestimmen, orthogonale Achsen zu ermitteln und die Beziehung zwischen den Ähnlichkeiten und den Distanzen zu visualisieren. Dabei werden n Punkte in n-1 Dimensionen repräsentiert, anschließend wird überprüft, welche Dimensionen entbehrt werden können.
Von Kruskal (1964) wurde eine Methode zur Dimensionsreduktion ermittelt, bei der die Anzahl der Dimensionen bereits vor der MDS-Analyse feststeht. Kruskal legte auch Wert darauf, die MDS-Analyse als Optimierungproblem zu betrachten: Er erstrebte eine (least square) Übereinstimmung zwischen einer monotonen Transformation der Daten und dem multidimensionalen Raum. Zur Optimierung werden die partiellen Ableitungen der Funktion nach jedem einzelnen Parameter des Modells berechnet und man folgt einer Prozedur des steilsten Abstiegs. Kruskal entwickelte Methoden für Daten mit und ohne Ties sowie auch für unvollständige Datenmatrizen (missing items).
Auch Guttman (1968) entwickelte und begründete Algorithmen zur nichtmetrischen MDS, die auf einem Optimalitätsindex beruhen und zu denen er auf mathematischem Wege eine Prozedur zur Optimierung des Optimalitätsindexes entwickelte (rank image transformations).
Coombs (1964) veröffentliche seine Theorie der Daten, die als Relationen zwischen Punkten im Raum betrachtet werden können und bei denen es sich um
Es wurden auch Methoden zur Berücksichtigung individueller Unterschiede entwickelt. Die Points-Of-View-Methode von Tucker und Messick (1962) bestimmt die Korrelationen der Ähnlichkeitsurteile der verschiedenen Personen, um eine Faktorenanalyse mit der Korrelationsmatrix durchzuführen. Deren Ergebnis ist der Personenraum, der zur Interpretation individueller Unterschiede dient, indem man nach Clustern von Personen sucht. Aus solchen Clustern werden dann hypothetische Distanzschätzungen generiert (points of view), die wiederum einer MDS unterzogen werden. Auf diese Weise werden individuelle Unterschiede allerdings nicht sparsam repräsentiert.
Eine bessere und weit verbreitete Berücksichtigung individueller Unterschiede wird durch den Ansatz von Carroll und Chang (1970) ermöglicht. Sie entwickelten eine Algortihmus zur gewichteten euklidischen MDS, bei der die einzelnen Achsen der MDS-Lösung für jede Versuchsperson individuell gewichtet werden können: Es wird von einem euklidischen Attributraum ausgegangen, dessen einzelne Dimensionen von jeder Versuchsperson unterschiedlich stark bei ihren Ähnlichkeitsurteilen gewichtet werden kann. Als Ergebnis der MDS wird jeder Versuchsperson ein Gewichtungsvektor zugewiesen. Geometrisch entspricht die Gewichtung einer Streckung bzw. Stauchung der Achsen des Lösungsraumes.
Die verschiedenen Methoden zur metrischen und nicht-metrischen und zur gewichteten und zur ungewichteten MDS können von dem Programm ALSCAL (alternating least squares scaling nach Takane, Young und Leeuw) berechnet werden, das auch Bestandteil von SAS und SPSS ist. Der zugrundeliegende Algorithmus kommt ohne Ableitungen aus und es werden quadrierte Entfernungen zwischen den Unähnlichkeiten eingesetzt; die Proximitäten können nominal, ordinal oder metrisch sein, die Matrizen können symmetrisch, asymmetrisch oder rechteckig sein und es dürfen einzelne Einträge der Matrizen fehlen. Eine Weiterentwicklung stellt der SMACOF-Algorithmus dar, der nicht von quadrierten Distanzen ausgeht und der effizienter zur Lösung findet.
Von Carroll und Chang (1972) stammt ein neuerer Ansatz, bei dem individuelle Differenzen sich auch in der Orientierung der Dimensionen ausdrücken können, wobei die Richtungen aber alle orthogonal zueinander sein müssen. Die Individuen können sich daher auch in ihrer Rotation des Reizraumes unterscheiden (zusätzlich zu unterschiedlichen Gewichtungen). Folgende weitere Ansätze zur MDS wurden entwickelt:
Eine letzte wichtige Weiterentwicklung besteht in der Maximum Likelihood MDS, die nicht nur deskriptive, sondern auch inferenzstatistische Schlüsse ermöglicht: Durch Signifikanztests kann die geeignete Dimensionalität bestimmt werden, das geeignete MDS-Modell sowie das geeignete Fehlermodell. Wichtig ist aber, daß die zugrunde gelegten Fehlermodelle (Normalverteilung oder log-Normalverteilung der Fehler; additive oder multiplikative Fehler) auch tatsächlich zutreffen, sonst sind die Signifikanzen nicht sinnvoll interpretierbar. Schließlich kann man auch postulieren, daß die Fehler nicht bei der Proximitäts-Schätzung, sondern bereits bei der Wahrnehmung der Reize auftreten. Schließlich gehen alle diese Modell davon aus, daß die Proximitätsurteile voneinander unabhängig sind.
Borg und Staufenbiel (1997) stellen sowohl die MDS als auch die Faktorenanalyse dar. Bei der Faktorenanalyse sollen Korrelationen von Variablen auf sparsame Weise beschrieben werden, wobei jede Variable in einem Vektormodell als das Resultat einer additiven Verknüpfung von einigen wenigen gemeinsamen Faktoren gedeutet wird.
Ausgangspunkt der Faktorenanalyse sind m Variablen, die an n Personen erhoben worden sind. Üblicherweise repräsentiert man die n Personen durch je einen Punkt im m-dimensionalen Variablenraum. Man kann aber auch die Variablen durch Vektoren im n-dimensionalen Personenraum darstellen. Standardisiert man die Variablen, indem man deren z-Werte berechnet, wird die Länge der Vektoren im Personenraum gleich Eins. Außerdem entspricht die Länge der Projektion eines Vektors auf einen anderen gleich der Korrelation der entsprechenden Variablen. Diese Korrelation läßt sich auch als ![]() berechnen, wobei
berechnen, wobei ![]() der Winkel zwischen den beiden Vektoren ist. Die Darstellung von ``vielen'' Variablen erfordert auch ``viele'' Dimensionen innerhalb des Personenraums, wenn die Winkel nicht in besonderer Weise zusammenpassen, indem sie beispielsweise innerhalb einer Ebene liegen.
der Winkel zwischen den beiden Vektoren ist. Die Darstellung von ``vielen'' Variablen erfordert auch ``viele'' Dimensionen innerhalb des Personenraums, wenn die Winkel nicht in besonderer Weise zusammenpassen, indem sie beispielsweise innerhalb einer Ebene liegen.
Bei der Hauptkomponentenanalyse geht man von den Korrelationen aller Variablen untereinander aus und versucht, diese Korrelationen durch eine Vektorkonfiguration im Personenraum darzustellen. Die Länge jedes Vektors wird durch die z-Standardisierung auf Eins normiert. Für alle vorgegebenen Korrelationen werden die Winkel zwischen den Vektoren bestimmt durch ![]() . Dann sucht man eine Vektorkombination, in der diese Winkel möglichst genau eingehalten werden.
. Dann sucht man eine Vektorkombination, in der diese Winkel möglichst genau eingehalten werden.
Im Idealfall kann man eine l-dimensionale (l < m) Vektorkombination finden, die die Korrelationen perfekt repräsentiert. Jeder Vektor kann dann durch die Angabe der Projektionswerte seiner Endpunkte (Ladungen) auf den gefundenen Koordinatenachsen (Faktoren) eindeutig bestimmt werden. Üblicherweise werden dabei die Koordinatenachsen orthogonal dargestellt. Die gefundene Konfiguration kann auch gedreht werden, da sich hierbei die Winkel nicht ändern. Man versucht, die Konfiguration so zu drehen, daß man eine Einfachstruktur erhält, bei der die Ladungen jedes Vektors auf allen Faktoren entweder groß (nahe Eins) oder klein (nahe Null) sind. Sind die Korrelationen aller Variablen untereinander nicht-negativ, dann werden auch die Ladungen aller Vektoren positiv oder gleich Null sein; dies entspricht der positive manifold hypothesis.
Man kann nun versuchen, eine höher-dimensionale Vektorkonfiguration so zu drehen, daß alle ihre Vektoren möglichst nahe an einer vorgegebenen Koordinatenachse liegen. Durch Projektion der Konfiguration entlang dieser Dimension auf den verbleibenden Rest-Raum kann man diese Dimension eliminieren. Diese Prozedur kann man für die verbleibenden Dimensionen schrittweise wiederholen. Die so extrahierten Koordinatenachsen nennt man Hauptachsen. Jede nächst-höhere Hauptachse erklärt die Vektoren zunehmend weniger genau. Anhand der Quadratsumme aller Vektorprojektionen bzw. Ladungen erhält man ein Maß für die erklärte Varianz, das ähnlich wie der Stress bei der MDS zu interpretieren ist. Mittels dieser erklärten Varianz kann man auch entscheiden, ab wann es sich nicht mehr lohnt, die Dimensionalität noch weiter zu erhöhen. Man bestimmt damit, wie viele Faktoren man beibehalten will und dreht diese Faktoren dann in einem zweiten Schritt in die optimale Einfachstruktur-Orientierung.
Eine Ladung entspricht gleichzeitig auch der Korrelation der Variablen mit dem jeweiligen Faktor (da es sich ja um ein Projektion einer standardisierten Größe auf diese Dimension handelt). Aufgrund der verschiedene Korrelationen eines Faktors kann man dann auch versuchen, diesen inhaltlich zu interpretieren, indem man sie beispielsweise mit Begriffen benennt, die das Gemeinsame der hoch auf sie ladenden Items ausdrücken.
Aus den Daten von N Personen bzw. n standardisierten Variablen extrahiert man also m Faktoren bzw. genauer die Ladungen der n Variablen ![]() auf den m Faktoren. Die Scores der Personen auf diesen Faktoren bezeichnet man als Faktor- oder Komponentenwerte. Diese Komponenten ergeben sich aus den Originalvariablen
auf den m Faktoren. Die Scores der Personen auf diesen Faktoren bezeichnet man als Faktor- oder Komponentenwerte. Diese Komponenten ergeben sich aus den Originalvariablen ![]() als gewichtete Summen; die Gleichung für die erste Hauptkomponente
als gewichtete Summen; die Gleichung für die erste Hauptkomponente ![]() lautet:
lautet:
![]()
wobei ![]() die Ladung der Variablen i auf der i-ten Hauptachse ist und
die Ladung der Variablen i auf der i-ten Hauptachse ist und ![]() den Variablenscore bezeichnet.
den Variablenscore bezeichnet.
Quadriert man die Ladungen einer Variablen, dann summieren sie sich (wegen der Standardisierung) im vollständigen Faktorenanalysen-Raum immer zu Eins, der Länge ihres Vektors. Das Quadrat jeder einzelnen Ladung gibt dagegen den durch den jeweiligen Faktor erklärten Varianzanteil an. Die Eigenwerte entsprechen der Summe der Quadrate der Ladungen (bezüglich einer Hauptachse) über alle Vektoren. Dividiert man die Eigenwerte durch die Anzahl der Vektoren, erhält man die durch die jeweilige Hauptachse aufgeklärte Varianz.
Verwendet man keine orthogonalen Koordinatensysteme, sondern schiefwinklige, dann korrelieren die Faktorwerte verschiedener Faktoren untereinander in Abhängigkeit von den Winkeln, die sie zueinander bilden. Diese Korrelationen kann man wiederum faktorenanalysieren. Diese Extraktion von Faktoren höherer Ordnung läßt sich im Prinzip weiter fortsetzen.
Im engeren Sinne spricht man nur dann von einer Faktorenanalyse, wenn man nicht die Korrelationen der beobachteten Werte analysiert, sondern nur die Korrelationen der Anteile, die jede Variable mit mindestens einer weiteren Variable gemeinsam hat (Kommunalitäten). Man will sich nämlich ganz auf die Korrelation der Variablen untereinander konzentrieren und spezifische Varianzen einzelner Variabler eliminieren (ähnlich wie bei den Spezifitäten bei der quasi-nichtmetrischen MDS). Technisch wird dieses Problem gelöst, indem man jede Variable durch multiple Regression aus allen anderen Variablen vorhersagt und nur mit diesem Teil weiterarbeitet.
Strukturgleichungsmodelle versuchen, Korrelations- und Kovarianzmatrizen durch ein Netzwerk von latenten Variablen (= Faktoren ) zu erklären. Dieses Netzwerk wird durch ein System linearer Gleichungen repräsentiert, in dem die beobachteten Variablen als gewichtete Summen der Faktoren erklärt werden, wo es aber außerdem möglich ist, Abhängigkeiten zwischen den Faktoren zu formulieren.
Borg und Staufenbiel (1997) stellen weitere wichtige Überlegungen zur multidimensionalen Skalierung vor. Sie beginnen damit, (geometrische) Distanzen zu algebraisieren, indem die euklidische Distanz bzw. eine andere Distanz nach der Minkowski-Metrik![]() zwischen Elementen einer Konfiguration bestimmt wird. Für die MDS-Lösung werden die Elemente dieser Lösung, also einzelne Punkte, solange im Raum verschoben, bis deren so berechnete Distanzen mit den Unähnlichkeiten zwischen den dadurch repräsentierten Reizen übereinstimmen. Der Grad der Übereinstimmung wird mit der Stress-Formel gemessen:
zwischen Elementen einer Konfiguration bestimmt wird. Für die MDS-Lösung werden die Elemente dieser Lösung, also einzelne Punkte, solange im Raum verschoben, bis deren so berechnete Distanzen mit den Unähnlichkeiten zwischen den dadurch repräsentierten Reizen übereinstimmen. Der Grad der Übereinstimmung wird mit der Stress-Formel gemessen:

Hierbei gelten folgende Schreibweisen:
Der Sinn einer MDS liegt in der inhaltlichen Deutung der Repräsentation. Borg und Staufenbiel (1997) geben folgende Hinweise für explorative dimensionale Deutungen: Man versucht, Achsen so durch die Punktekonfiguration der MDS-Lösung zu legen, daß Punkte, die inhaltlich etwas gemeinsam haben, auch ähnliche Werte auf der entsprechenden Achse zugewiesen bekommen und Punkte, die wenig gemeinsam haben, unterschiedliche Werte erhalten. Bei dem explorativen Vorgehen gelangt man auf diese Weise zu einem System an Dimensionen.
Statt rein explorativ vorzugehen, kann man im Rahmen der MDS auch vermutete Dimensionssysteme testen. In diesem Zusammenhang spricht man von einem konfirmatorischen Vorgehen. Dazu kann man beispielsweise die Dimensionen, die mittels einer MDS aus Ähnlichkeitsurteilen erhoben wurden, mit Einstufungen derselben Items auf externen Skalen (die beispielsweise durch einen Fragebogen erhoben werden) vergleichen. Dabei wird die MDS-Lösung so gedreht, daß die Korrelation zwischen den gefundenen Dimensionen (bzw. den Koordinaten der Items auf der entsprechenden Dimension) und den vorgegebenen Skalen maximal wird. Auf rechnerischem Wege kann man auch versuchen, die externen Skalen durch (multiple) Regression aus den Dimensionen (die auch als interne Skalen bezeichnet werden) vorherzusagen. Damit läßt sich überprüfen, ob die externen (Fragebogen-)Skalen sich auch zur Erklärung der Unähnlichkeitsurteile eignen.
Dimensionale Interpretationen von MDS-Lösungen sind aber nicht die einzig möglichen; es handelt sich dabei vielmehr um Spezialfälle von allgemeineren Organisationsprinzipien. Borg und Staufenbiel (1997) schlagen daher vor, den Lösungsraum zu partitionieren, d.h. in Regionen zu zerteilen, die aufgrund inhaltlicher Gemeinsamkeiten definiert sind. Als Beispiel führen sie die Partitionierung einer MDS-Lösung für Morsecodes an: Der Lösungsraum läßt sich anhand von drei Kriterien partitionieren:
Man kann aber nicht nur versuchen, eine MDS-Lösung nachträglich zu partitionieren, sondern man kann auch prüfen, ob sich - durch Theorien vorgegebene - Partitionen (also ``geschlossene'' Regionen) finden lassen. Ein Beispiel wäre eine Radex-Organisation der Lösung, bei der der Lösungsraum in ``Kreissegmente'' aufgeteilt wird, die bestimmten theoretischen Konzepten entsprechen. In diesem Falle wäre eine dimensionale Deutung ungeeignet.